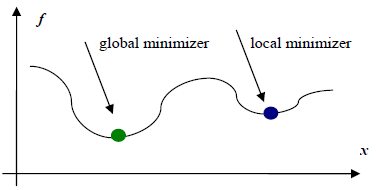
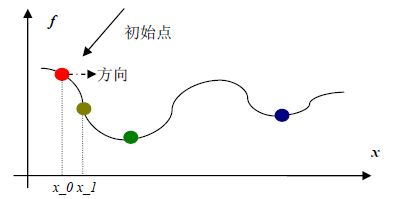
上一篇文章介绍了梯度下降相关的优化方法，这一篇来介绍一个在优化领域也用的非常多的方法，牛顿法和拟牛顿法

0.Hesse 矩阵

Hesse矩阵在牛顿法中常被用到，它的本质就是二维偏导的矩阵，形式如下所示：

1.牛顿法

之前介绍的梯度下降法，只考虑了目标函数的一阶导数信息，而牛顿法择一并考虑二阶导数信息。
设$f(x)$为具有二姐连续偏导数的目标函数，第$k$次迭代值为$x_k$，在$x_k$处进行二阶泰勒展开：

$$f(x)=f(x_k)+g_k^T(x-x_k)+\frac{1}{2}(x-x_k)^TH(x_k)(x-x_k)$$

$g_k$是$f(x)$的梯度向量在点$x_k$处的值，$H(x_k)$是$f(x)$的Hesse矩阵在点$x_k$处的值。
由于极小值点必然是一阶导数为0的点，所以我们令$f(x)$的一阶导数等于0，求上面那个泰勒展开式的导数：

$$\nabla{f(x)}=g_k+H_k(x-x_k)$$

在机器学习领域，优化方法一直是一个很重要的领域，最常见的就是利用目标函数的导数通过多次迭代来求解无约束最优化问题，那么什么是无约束最优问题，又有那些方法来求解呢？下面我就分两篇文章来分别讲一下最常见的两类求解方法。

0.无约束最优化

那么到底什么是无约束最优化呢？这里举一个栗子来说明一下，看下面这张图。

上图所示为意愿函数f(x)的图像，无约束最优化问题，即不对定义域或值域做任何限制的情况下，求解函数f(x)的最小值，上面显示两个最小值点：一个为全局最小值点，另一个为局部最小值点。受限于算法复杂度等问题，目前大部分无约束最优化算法只能保证求取局部最小值点。这时读者不免要问，既然只能求取局部最小值点，那为什么这类算法还能应用呢。这是因为实际应用中，许多情形被抽象为函数形式后均为凸函数，对于凸函数来说局部最小值点即为全局最小值点，因此只要能求得这类函数的一个最小值点，该点一定为全局最小值点。
理解了上面的无约束最优化问题之后，我们就可以开始介绍无约束最优化的求解过程了，对于无约束最优化的求解首先我们需要选择一个初始点x_0，如下所示：

初始点选择好之后，就可以按照各种不同的无约束最优化求解算法，求解最小值点了。求解过程中主要涉及两个概念，即从初始点开始沿“哪个方向”以及“走多远”到达下一个点处。所谓“走多远”即之前提的“步长”的概念，“哪个方向”即方向概念。
下面我就介绍一种最常用的一种选择方向的方法，即选择梯度作为方向。

C++ 标准库中现在存在两种形式的Key-Value容器，map和unordered_map。
unordered_map是C++ 11后面新加入标准库的。

主要区别：
map:它是有序的，内部实现是一颗红黑树，相比unordered_map内存消耗少,因为unordered_map有一个巨大的数组，也就是哈希表，会有很多空间的浪费。
unordered_map:无序，通过哈希函数来生成key，插入和删除，查询的效率更高，但是需要注意的一点是如果提前不知道unordered_map的size，没有reserve的话，那么插入的时候会经常不断的reserve，那么所有的元素都需要rehash，这是比较耗时的。

还有一个需要注意的地方，map比unorderd_map要更加稳定，在循环迭代输出的时候，map要比unordered_map更快。