在机器学习领域,优化方法一直是一个很重要的领域,最常见的就是利用目标函数的导数通过多次迭代来求解无约束最优化问题,那么什么是无约束最优问题,又有那些方法来求解呢?下面我就分两篇文章来分别讲一下最常见的两类求解方法。
0.无约束最优化
那么到底什么是无约束最优化呢?这里举一个栗子来说明一下,看下面这张图。
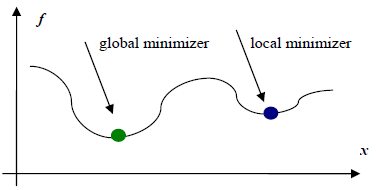
上图所示为意愿函数f(x)的图像,无约束最优化问题,即不对定义域或值域做任何限制的情况下,求解函数f(x)的最小值,上面显示两个最小值点:一个为全局最小值点,另一个为局部最小值点。受限于算法复杂度等问题,目前大部分无约束最优化算法只能保证求取局部最小值点。这时读者不免要问,既然只能求取局部最小值点,那为什么这类算法还能应用呢。这是因为实际应用中,许多情形被抽象为函数形式后均为凸函数,对于凸函数来说局部最小值点即为全局最小值点,因此只要能求得这类函数的一个最小值点,该点一定为全局最小值点。
理解了上面的无约束最优化问题之后,我们就可以开始介绍无约束最优化的求解过程了,对于无约束最优化的求解首先我们需要选择一个初始点x_0,如下所示:
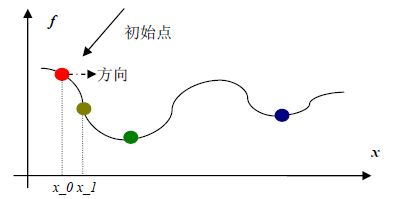
初始点选择好之后,就可以按照各种不同的无约束最优化求解算法,求解最小值点了。求解过程中主要涉及两个概念,即从初始点开始沿“哪个方向”以及“走多远”到达下一个点处。所谓“走多远”即之前提的“步长”的概念,“哪个方向”即方向概念。
下面我就介绍一种最常用的一种选择方向的方法,即选择梯度作为方向。
1.梯度下降法
梯度下降法(或最速下降法)是求解无约束优化问题的一种最常用的方法,假设$f(x)$是$R^*$上具有一阶连续偏导数的函数,需要求解的无约束最优化问题是
$$\min_{x\varepsilon R^n}f(x)$$
$x^*$是目标函数的极小值点.
梯度下降法是一种迭代算法,选取适当的初值$x^{(0)}$,反复迭代,更新$x$的值,进行目标函数的极小化,直至收敛。由于我们都知道梯度方向是函数增长最快的方向,那么自然而然的想到负梯度方向就是函数值下降最快的方向了。因此,我们以负梯度方向作为极小化的下降方向,在迭代的每一步,以负梯度方向来更新$x$的值,从而达到减小函数值目的,这种方法就是梯度下降法(也叫最速下降法)。
由于$f(x)$具有一阶连续偏导数,若第$k$次迭代值为$x^{(k)}$,则可将$f(x)$在$x{(k)}$处进行一阶泰勒展开:
$$f(x)=f(x^{(k)})+g_k^T(x-x^{(k)})$$
这里,$g_k=g(x^{(k)})=\nabla{f(x^{(k)})}$为$f(x)$在$x^{(k)}$的梯度。
第$k+1$次迭代值$x^{(k+1)}$:
$$x^{(k+1)} = x^{(k)}+\lambda_kp_k$$
其中,$p_k$是搜索方向,取负梯度方向$p_k$=$-\nabla{f(x^{(x)})}$,$\lambda_k$是步长,有时候我们也叫学习率,这个值可以由一维搜索确定,即$\lambda_k$使得
$$f({x^{(k)}+\lambda_kp_k})=\min_{\lambda\geq0}f({x{(k)}+\lambda p_k})$$
即令导数为零找到该方向上的最小值,但是在实际编程中,这样计算的代价太大,我们一般可以将它设定为一个常量。
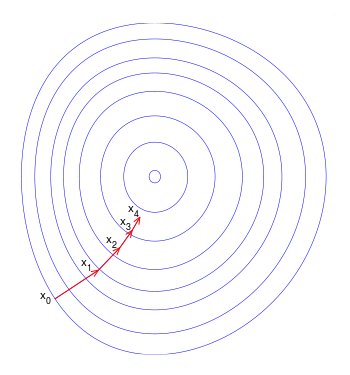
如果目标函数是一个凸优化问题,那么最速下降法得到的是全局最优解,否则,它有可能求得的只是一个局部最优解,理想的优化效果如下图所示。注意:每一次迭代的移动方向都与出发点的等高线垂直:
但是,在某些情况下,最速下降法是存在锯齿现象的,这将会导致收敛速度变慢:
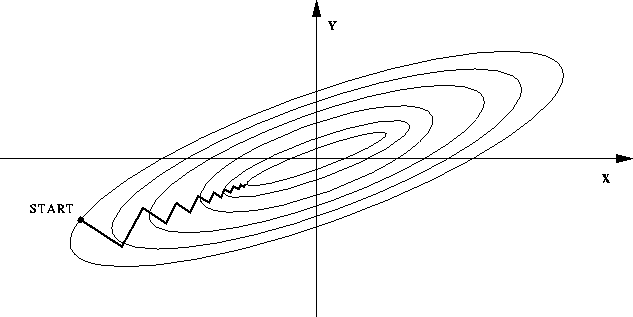
造成这种情况是因为在二次函数中,等高线椭球面的形状受 hesse 矩阵的影响,椭球面的长轴与短轴对应矩阵的最小特征值和最大特征值的方向,其大小与特征值的平方根成反比,最大特征值与最小特征值相差越大,椭球面越扁,那么优化路径需要走很大的弯路,计算效率很低。
需要注意的是,最速下降法是每次迭代都需要计算全部样本值的梯度的,而在实际求解过程中,它的收敛速度是比较慢的,是一阶收敛。所以就出现了下面两种方法。
2.共轭梯度下降法
要了解共轭梯度下降法,首先要知道什么是共轭。设$G$为对称正定矩阵,若$a_m^TGa_n$,则称$a_m$和$a_n$为“$G$共轭”。当G为单位向量时,有$a_ma_n=0$,所以“共轭”是“正交”的推广。
那么沿着一系列的共轭方向做迭代,这些共轭方向组成的集合叫做共轭方向集,这既是共轭方向法。即对于二次正定目标函数,从任意点$x_0$出发,沿任意下降方向$a_m$做直线搜索得到$x_1$,沿与$a_m$共轭的方向$a_n$做直线搜索,反复迭代,即可得到目标函数的极小值点。
另外,还有一个概念要搞清楚,就是二次收敛性。
当目标函数是二次函数时,共轭方向法最多经过N步(N为向量维数)迭代,就可以到达极小值点——这种特性就是二次收敛性。(注:最下降法和随机梯度下降法为一次收敛)
那么,是不是当目标函数不是二次函数的时候,共轭方向法就失效了呢?答案是否定的,可以证明,将二次收敛算法用于非二次的目标函数时,也有很好的效果。但是,这个时候就不能保证N步迭代到达极小值了。
关于迭代的方式跟前面的最速下降法类似,在此不再赘述,这里的关键问题是如何产生一组关于$G$共轭的向量,有个常用的方法是Gram-Schmidt的方法。
取线性无关的向量组$v_0,v_1,v_2,…,v_{n-1}$,取$p_0=v_0$
$$p_{k+1}=v_{k+1}-\sum_{j=0}^k \frac{(p_i)^TGv_{k+1}}{(p_i)^TQp_i}p_i$$
上面的方法是针对目标函数为正定二次函数的,而对于一般的非二次函数,可以通过泰勒展开的二次近似。
而共轭梯度法是共轭方向法的一种延伸,初始的共轭向量$p_0$由初始点的负梯度$-g_0$给出,以后的$p_k$由当前迭代点的负梯度与上一个共轭向量的线性组合来确定:
$$p_{k+1}=-g_{k+1}+a_kp_k$$
$a_k$是迭代步长,$a_k=\frac{\left | g_{k+1} \right |^2}{\left |g_k \right |^2}$,对于非二次函数的优化问题,迭代次数不止n次,但共轭方向只有n个。当迭代n次后,可以把$p_n$ 重新置为最开始的 $p_0$,其他的变量按照原方法更新。
3.随机梯度下降法
说了最速下降法,共轭梯度下降法,那么随机梯度下降法又是什么呢?随机梯度法是在深度学习里面用的最多的一种优化方法,为什么深度学习用的最多的是这种方法而不是最速下降法或者共轭梯度法呢?下面就来解释一下这个问题。
与最速下降法相比,最速下降法每次迭代都要计算所有训练集的梯度,如果训练集很大,可想而知,这种方法的效率会非常的低下,所以随机梯度下降法应运而生,随机梯度下降法是通过每次计算一个样本来迭代更新,那么可能只需要几百或者几千个样本,就可以得到最优解了,相比于上面的最速下降法和共轭梯度法,迭代一次需要全部的样本,这种方法效率自然就较高。
但是,与此同时,随机梯度下降法由于每次计算只考虑一个样本,使得它每次迭代并不一定都是整体最优化方向。如果噪声较多,很容易陷入局部最优解。
4.总结
- 最速下降法收敛速度慢,共轭梯度法其次,随机梯度法最快
- 最速下降法和共轭梯度法每次更新都需要用到所有样本,而随机梯度法只需要计算单个样本
- 最速下降法优于使用真正的梯度,每一次权值更新的步长较随机梯度下降要大
- 随机梯度下降如果噪声较多会陷入局部极小值
- 共轭梯度法是介于最速下降法和牛顿法之间的一个方法,克服了最速下降法收敛慢的特点,也避免了牛顿法需要计算Hesse矩阵的缺点。
5.参考
(1)http://www.cnblogs.com/daniel-D/p/3377840.html
(2)http://www.codelast.com/?p=8006
(3)http://www.codelast.com/?p=2348