这篇论文的下载地址,这篇论文主要解决的是在汉明空间上的r-neighbors of query和K-NN query,提出了一种新型的多分段索引哈希方法,比传统的linear scan的速度快了100倍。
1.多分段索引哈希
它的主要思想是:
对于一个哈希码h,一共有b位,将它分为m段,那么,每段的长度为$\lfloor b/m\rfloor$或者$\lceil b/m \rceil$,为了方便起见,我们假设b能够被m整除,下位直接用$b/m$代替,那么当两个哈希码h和g的汉明距离为r bits的时候,在这m段哈希码中必然至少存在一段,它们之间的汉明距离最多为$\lfloor r/m \rfloor$。
那么基于这个思想,我们可以在查询与哈希码h的汉明距离为r的所有哈希码时,我们可以分别对这m段哈希码进行查找,找出在每一段哈希码中,汉明距离小于$\lfloor r/m \rfloor$的查询结果,将m段的查询结果合并之后就是我们最终的候选集,最后在候选集中筛选出汉明距离大于r的结果。这种方法相比于线性搜索的需要查找$L(b,r)$个桶的情况,现在我们只需要搜索$m*L(b/m,\lfloor r/m \rfloor)$个哈希桶,大大提高了查询效率。
2.query and storage cost
查询的cost,每次查询需要查找哈希桶的查找次数为
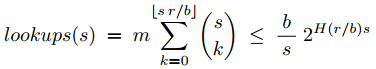
对于一次查询所需要的总查询次数为上面求出的lookups和最后筛选的cost之和,所以可以得出,每次查询的cost:
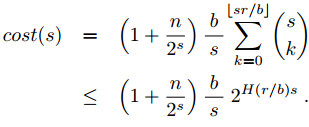
这种图表示了在不同条件下的cost的对比:
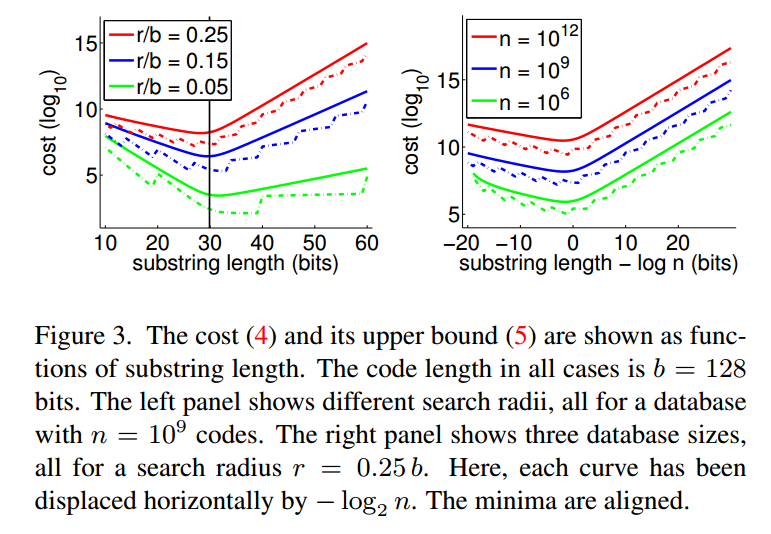
存储cost,考虑一共有n个b位的哈希码,分为m段,那么就有m个哈希table,存储所有的哈希码就需要$O(nb)$,对于m个哈希表,我们存储着n个哈希码的索引,那么对于n个哈希码来说还额外需要$O(mnlog_2n)$bits,所以,存储cost一共需要$O(nb+mnlog_2n)$。
3.KNN查询
上面所说的是r-neighbors查询,但是对于实际的需要中,我们很多时候不关心r,我们关心的是返回查询结果的前k个,那么这种情况该怎么做呢?论文首先通过以下这种图来说明在不同取值k的情况下,汉明距离分布的不均匀性。
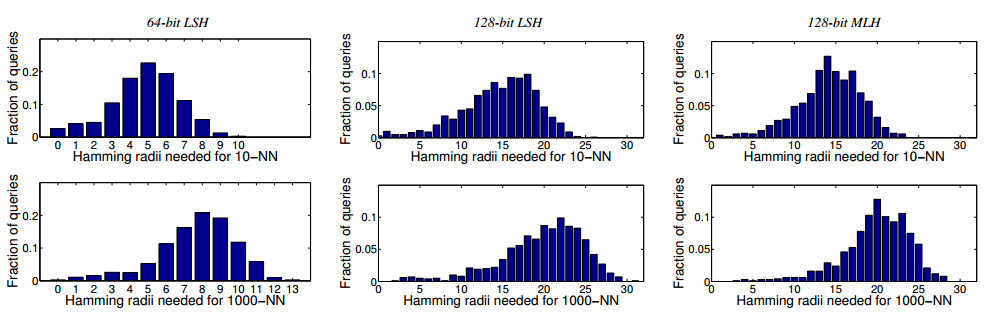
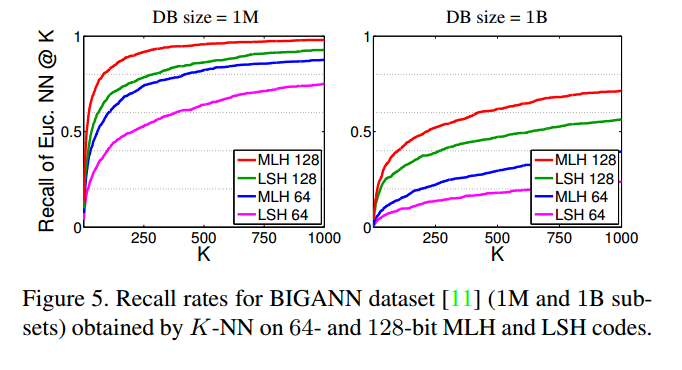
然后,它提出了查询KNN的方法,分别对m段哈希码逐步增加查询半径r的取值,当查询结果大于k的时候停止查询,将所有的查询结果合并,筛选出前K个结果,实验结果如下:
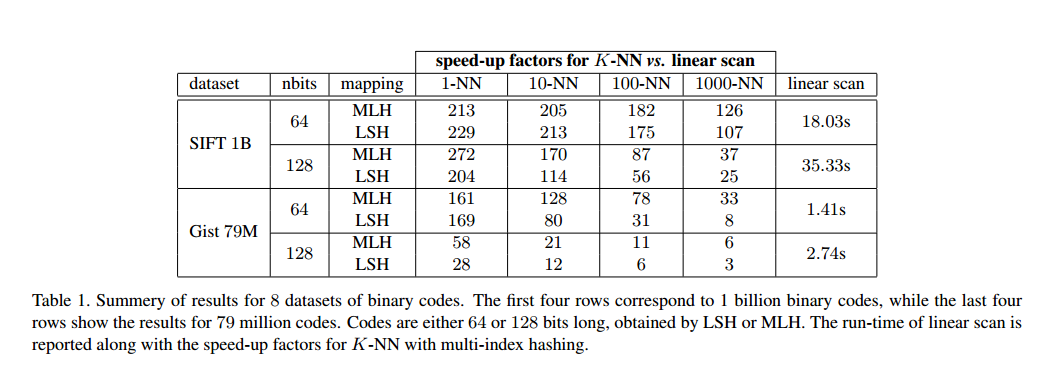
召回率
用LSH和MLH两种产生哈希的方法来测试,由此可以看出,这种方法的查询时间也受哈希分布的影响
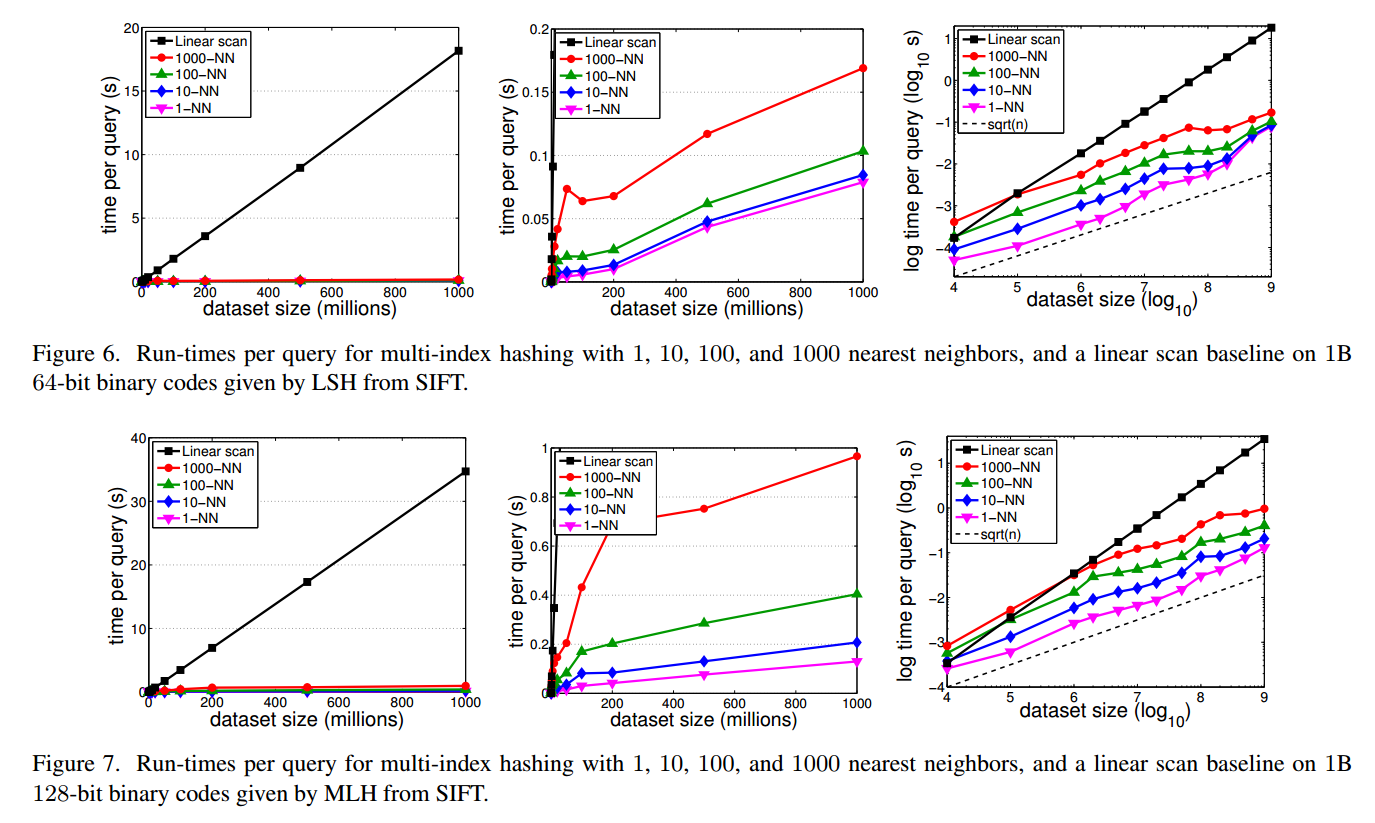
总结
这篇论文的思想与前面所提到的的simhash的方法很相似,只不过simhash是对前面的一部分精确匹配,这篇论文是对每一段都是模糊匹配,方法较linear scan有较大的效率提升,并且存储的复杂度也不是特别高,作者也把实现代码开源了。