上一篇文章介绍了梯度下降相关的优化方法,这一篇来介绍一个在优化领域也用的非常多的方法,牛顿法和拟牛顿法
0.Hesse 矩阵
Hesse矩阵在牛顿法中常被用到,它的本质就是二维偏导的矩阵,形式如下所示:

1.牛顿法
之前介绍的梯度下降法,只考虑了目标函数的一阶导数信息,而牛顿法择一并考虑二阶导数信息。
设$f(x)$为具有二姐连续偏导数的目标函数,第$k$次迭代值为$x_k$,在$x_k$处进行二阶泰勒展开:
$$f(x)=f(x_k)+g_k^T(x-x_k)+\frac{1}{2}(x-x_k)^TH(x_k)(x-x_k)$$
$g_k$是$f(x)$的梯度向量在点$x_k$处的值,$H(x_k)$是$f(x)$的Hesse矩阵在点$x_k$处的值。
由于极小值点必然是一阶导数为0的点,所以我们令$f(x)$的一阶导数等于0,求上面那个泰勒展开式的导数:
$$\nabla{f(x)}=g_k+H_k(x-x_k)$$
那么,由$\nabla{f(x)}=0$,得
$$g_k+H_k(x-x_k)=0$$
可知,当$H_k$为非奇异矩阵的时候,它的逆矩阵存在,两边同乘逆矩阵,迭代公式即为
$$x=x_k-H_k^{-1}g_k=x_k+d$$
$$H_kd=-g_k$$
用上面方法作为迭代公式的算法就是牛顿法,一般认为牛顿法可以利用到曲线本身的信息,比梯度下降法更容易收敛(迭代次数更少),下图就是一个最小化目标方程的例子,红色曲线是利用牛顿法迭代求解,绿色曲线是利用梯度下降法求解。
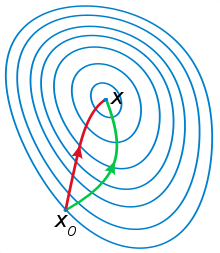
这种牛顿法虽然具有二次收敛性,但是要求初始点需要尽量靠近极小点,否则有可能不收敛。计算过程中需要不断计算目标函数的二阶偏导数,计算量大。而且Hesse矩阵无法一直保持正定,会导致算法产生的方向不能保证是$f(x)$在$x_k$处的下降方向,从而牛顿法失效(只有Hesse矩阵正定,才能保证$f_x$在$x_k$处下降)。
正是由于牛顿法上面的这些限制,所以才有了拟牛顿法。
2.拟牛顿法
拟牛顿法的基本思想是不计算二阶偏导数,构造出一个近似Hesse的逆矩阵的正定对称阵,从而根据这个近似矩阵来优化目标函数。不同的近似阵构造方法决定了不同的拟牛顿法。
设$f(x)$二次连续可微,$f$在$x_{k+1}$附近的泰勒展开近似即为
$$f(x)=f(x_{k+1})+g_k^T(x-x{k+1})+\frac{1}{2}(x-x{k+1})^TH_{k+1}(x-x_{k+1})$$
两边同时求导
$$g(x)=g_{k+1}+H_{k+1}(x-x_{k+1})$$
取$x=x_k$
$$g_k=g_{k+1}+H_{k+1}(x_k-x_{k+1})$$
$$g_k-g_{k+1}=H_{k+1}(x_k-x_{k+1})$$
记$y_k=g_{k+1}-g_k$,$\delta_k=x_{k=1}-x_{k}$
$$y_k=H_{k+1}\delta_k$$
或
$$H_{k+1}^{-1}y_k=\delta_k$$
上面两个公式即为拟牛顿条件。按照拟牛顿条件选择$G_k$作为$H_k^{-1}$的近似或者选择$B_k$作为$H_k$的近似的算法称为拟牛顿法。
按照拟牛顿条件来更新矩阵$G_{k+1}$
$$G_{k+1}=G_k+\Delta{G_k}$$
更新$G_k$之后,将$G_k$作为$H^{-1}$的近似或者$B_k$作为$H$的近似,然后根据$H_kd=-g_k$,即可算出$d$的值。
2.1 DFP算法
DFP算法选择$G_{k+1}$的方法是在$G_k$加上两个附加项构成的,即
$$G_{k+1}=G_k+P_k+Q_k$$
其中,$P_k$,$Q_k$是待定矩阵,为了使$G_{k+1}$满足拟牛顿条件,可使$P_k$和$Q_k$满足:
$$P_ky_k=\delta{k}$$
$$Q_ky_k=-G_ky_k$$
具体的求解过程此处从略,可取
$$P_k=\frac{\delta{_k}\delta{_k}^T}{\delta{_k}^Ty_k}$$
$$Q_k=-\frac{G_ky_ky_k^TG_k}{y_k^TG_ky_k}$$
这样就得到了矩阵$G_{k+1}$的迭代公式:
$$G_{k+1}=G_k+\frac{\delta{_k}\delta{_k}^T}{\delta{_k}^Ty_k}-\frac{G_ky_ky_k^TG_k}{y_k^TG_ky_k}$$
称为DFP算法。
2.2 BFGS算法
可以考虑用$B_k$来逼近Hesse矩阵$H$,这时,拟牛顿条件为
$$B_{k+1}\delta{_k}=y_k$$
同样的,
$$B_{k+1}=B_k+P_k+Q_k$$
$$P_k\delta{_k}=y_k$$
$$Q_k\delta{_k}=-B_k\delta{_k}$$
找出符合条件的$P_k$和$Q_k$,得到BFGS算法矩阵的迭代公式:
$$B_{k+1}=B_k+\frac{y_ky_k^T}{y_k^T\delta_k}-\frac{B_k\delta_k\delta_k^TB_k}{\delta_k^TB_k\delta_k}$$
3.总结
- 牛顿法是二阶收敛,收敛速度更快
- 牛顿法每次计算都需要计算目标函数的二阶偏导数,难度较大,并且无法保证Hesse矩阵的正定性
- 牛顿法是用一个二次曲面去拟合当前所处位置的局部曲面,而梯度下降法是用一个平面去拟合当前的局部平面,通常情况下,二次曲面的拟合会比平面更好,所以牛顿法选择的下降路经会更符合真实的最优下降路经
- 拟牛顿法不需要计算二阶偏导数,用近似矩阵来代替Hesse矩阵
4.参考
(1).http://blog.csdn.net/chlele0105/article/details/38895711
(2).http://www.codelast.com/?p=2780