Simhash算法原理

这篇文章简单的对simhash做个记录，因为已经有很多文章都写的非常好了，类似参考文献1和参考文献2，simhash是当年google用来文本去重的算法，大致思想就是将一个文档转换成一个n位的字节，然后判断两篇文章的字节码的汉明距离，如果小于某个给定的阈值就说明它们两个相似。那么由此可以看出，它分为两个部分，一个是n位字节码的生成，另一个是汉明距离的比较。

1.特征字节的生成

引用这张经典的原理图：

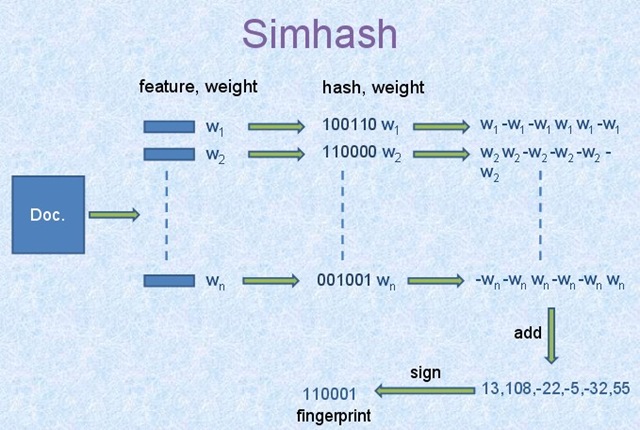
它的算法流程如下：

1.选择simhash的位数，例如32位或64位；
2.将Doc文件进行分词，并赋予权重，赋予权重的方法有很多重，可以根据词频等信息的一些方法。将每个关键词转换为对应位数的哈希码，在这里，我们假设我们的哈希位数为6，那么依据图中信息可知n个词的哈希码如上面100110,110000…；
3.然后对这n个哈希码按列相加，如果哈希码为1，那么+weight，反之-weight，计算最后生成的结果，如上图所示的[13,108,-22,-5,-32,55]；
4.然后由[13,108,-22,-5,-32,55]转换成最终的哈希码[1,1,0,0,0,1]，正取1，负取0。

好，以上就是我们生成哈希码的过程，那么得到哈希码之后，如何从海量文本中查询汉明距离为r的文本呢？

2.索引查询

假设在这里，我们要查询汉明距离为3以内的数据，那么只要我们将整个64位的哈希码分为4块，无论如何，在满足汉明距离为3的情况下，至少有一段两个哈希码是完全相同的。

所以基于以上思想，在刚才那个例子的情况下，我们可以设计出如下算法，将64位哈希码分成4份，并需要将这64位哈希码存储为4份table，分别变换精确匹配的位置，来查找前16位哈希码完全相同的记录作为候选记录，如下图所示：

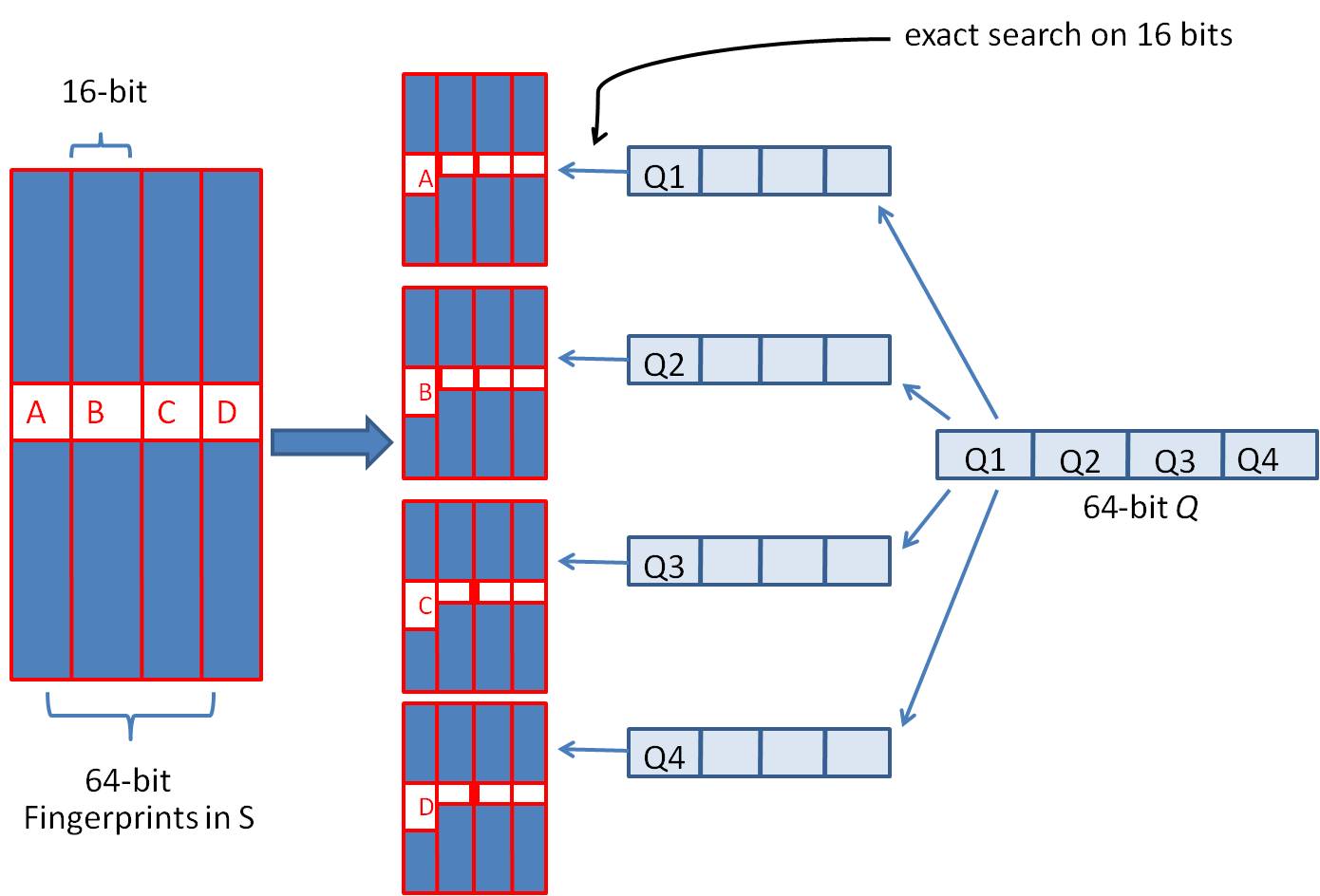
具体的算法过程如下：

1.将64为哈希码分为4份；
2.调整这4段哈希码的位置，分别将这四种情况存储在4分table中；
3.采用精确匹配的方法查找前16位哈希码
4.如果样本库中存有$2^{34}$（差不多10亿）的哈希指纹，则每个table返回$2^{(34-16)}=262144$个候选结果，大大减少了海明距离的计算成本。

那么有人可能会问，那分为5段的话又是怎么查询呢？
分为5段的话，那么需要$C_5^3=10$个哈希表来存储，每段哈希码大约为$64/5=13$位，分别变换这5段哈希码的位置，存储为10份哈希表，每次精确匹配前两段，那么10个哈希表分别会返回$2^{(34-13*2)}$个结果。同理，分为6段的话，那么需要$C_5^3$=20个哈希表来存储，每段哈希码大约为$64/6=11位哈希码$，那么每段返回的结果会更少。
可知，时间与空间的效率不可兼得，选择一个合适的分段数是很重要的。

另外，这里还提供一个比较两段哈希码汉明距离的代码：

int calHammingDis(uint64_t lhs, uint64_t rhs){

    int cnt = 0;
    lhs ^= rhs;
    while(lhs)
    {
        lhs &= lhs - 1;
        cnt++;
    }
    return cnn;
}

其实在这里，我们看到simhash的一个弊端，它的分段数必须大于查询的汉明距离，不然就失去了作用。
另外，还写了一篇multi-index-hash的文章的思想与这篇的思想很像，可以一起对照来看。

参考文献

[1]: http://grunt1223.iteye.com/blog/964564
[2]: http://yanyiwu.com/work/2014/01/30/simhash-shi-xian-xiang-jie.html
[3]: http://tangxman.github.io/mih/