在上篇文章中对比了中文词语粗分的几个算法,提到N-最短路径算法在中文词语粗分中的优势,下面在这篇文章中就着重研究N-最短路径算法的原理。
首先我们要知道,N-最短路径算法中的N指的是什么?
_N指的是从源点到终点的前N条最短路径长度的若干条路径,这里有个地方要注意的是N指的是前N条最短路径长度。_例如:求2-最短路径,从源点到终点的最短路径长度为5,次短路径长度为6,但是包含最短路径长度的不一定就只有一条路径,譬如可能有两条路径A,B都是路径长度为5,又有三条路径C,D,E的长度为6,那么求2-最短路径即求A,B,C,D,E这五条路径。这个问题清楚之后,我们就开始下面的问题。
在了解N-最短路径之前,首先,我们来看看1-最短路径算法。顾名思义,1-最短路径即求的是最短路径,下面我们来看看1-最短路径是如何实现的:
一、数据表示
我们用如下的有向图来举例说明,各权重已标明:
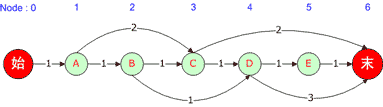
(图一)
根据有向图可以建立如下所示的二维表:
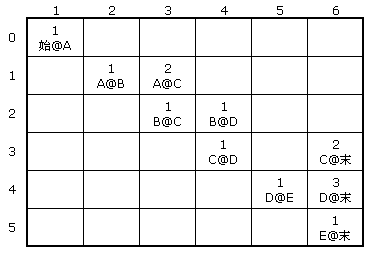
(图二)
二、求出PreNode
要求出源点到该点最短路径的PreNode链表,可根据Dijkstra算法求出源点到每个点的最短路径及其PreNode,求解过程略,可得到如下图所示的PreNode链表:
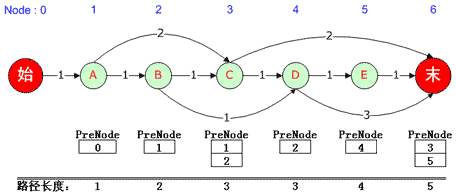
(图三)
说明:该点有多个PreNode,是因为源点到该点的最短路径可能不止一条,因此会有多个PreNode,例如:从源点到C的最短路径为3,但是有两条路径可取到最短路径,所以C的PreNode有两个,一个是A,一个是B。
三、求1-最短路径
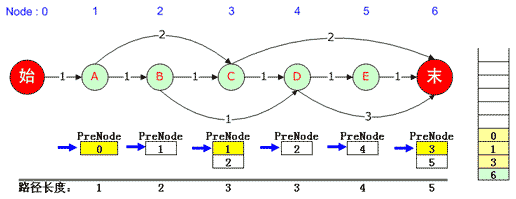
(图四)
算法思想如下:
- 首先将最后一个节点入栈(本例中即为6号节点),作为结束节点,当该节点出栈时,算法结束。
- 对于每个节点的PreNode队列,维护了一个当前指针,初始状态都指向PreNode的第一个元素。
- 从右至左一次取出当前指针所指的PreNode节点,例如:6的PreNode是3,3的PreNode是1,1的PreNode是0,那么栈内元素即为0->1->3->6,如上图所示。
- 当源点(本例中即为0号节点)入栈时,即得到一个最短路径0->1->3->6。
- 以此弹出栈中内容,每弹出一个元素,就将当时压栈时对应的PreNode队列指针向后移一位,如果当了末尾无法下移,则继续执行第5步;否则,执行第3步。
对于本例,先将“0”弹出堆栈,该元素对应的是1号“A”结点的PreNode队列,该队列的当前指针已经无法下移,因此继续弹出堆栈中的“1” ;该元素对应3号“C”结点,因此将3号“C”结点对应的PreNode队列指针下移。由于可以移动,因此将队列中的2压入队列,2号“B”结点的PreNode是1,因此再压入1,依次类推,直到0被压入,此时又得到了一条最短路径,那就是0,1,2,3,6。如下图:
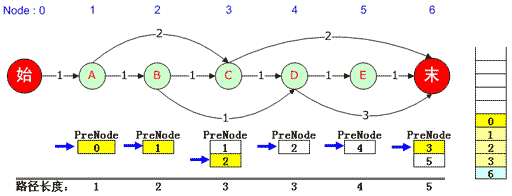
(图五)
再往下,0、1、2都被弹出堆栈,3被弹出堆栈后,由于它对应的6号元素PreNode队列记录指针仍然可以下移,因此将5压入堆栈并依次将其PreNode入栈,直到0被入栈。此时输出第3条最短路径:0, 1, 2, 4, 5, 6。入下图:
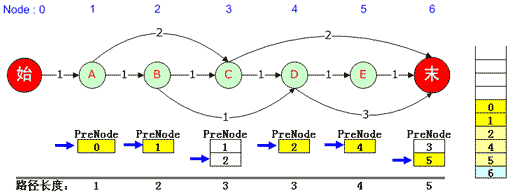
(图六)
输出完成后,紧接着又是出栈,此时已经没有任何堆栈元素对应的PreNode队列指针可以下移,于是堆栈中的最后一个元素6也被弹出堆栈,此时输出工作完全结束。我们得到了3条最短路径,分别是:
- 0, 1, 3, 6,
- 0, 1, 2, 3, 6,
- 0, 1, 2, 4, 5, 6,
四、总结
- N-最短路径的求解比较复杂,本文先从求解1-最短路径着手,说明SharpICTCLAS是如何计算的,在下篇文章中将推广到N-最短路径。
- 1-最短路径并不意味着只有一条最短路径,而是路径最短的若干条路径。就如本文案例所示,1-最短路径算法最终求得了3条路径,它们的长度都是5,因此都是最短路径。