在这里把上周讨论的Maxout和Network in Network整理一下。
关于Maxout的论文为:http://jmlr.org/proceedings/papers/v28/goodfellow13.pdf
我们常见的隐含层节点输出:
$$h_i(x)=sigmoid(x^TW_{…i}+b_i)$$
而在Maxout网络中,其隐含层节点的输出表达式为:
$$h_i(x)=\max_{j\in[1,k]}z_{ij}$$
where$z_{ij}=x^TW_{…ij}+b_{ij}$,and $W\in{R^{dmk}}$
这里的W是3维的,尺寸为dmk,其中d表示输入层节点的个数,m表示隐含层节点的个数,k表示每个隐含层节点对应了k个”隐隐含层”节点,这k个”隐隐含层”节点都是线性输出的,而maxout的每个节点就是取这k个”隐隐含层”节点输出值中最大的那个值。因为激发函数中有了max操作,所以整个maxout网络也是一种非线性的变换。
类似下面这张图:
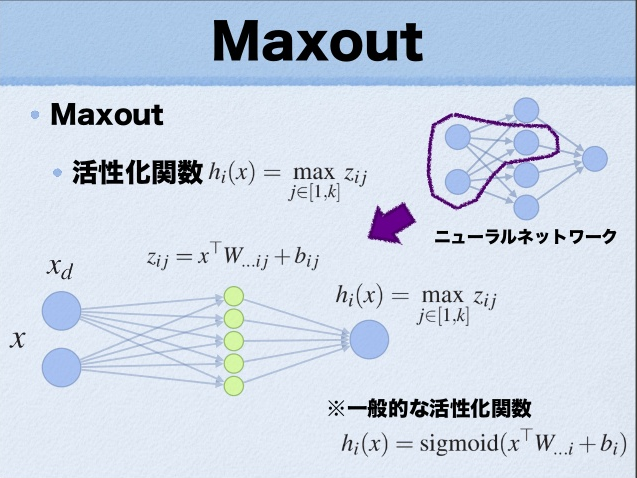
如果还是不太清楚的话,看这个渣手绘(请原谅我丑陋的绘画 /(ㄒoㄒ)/~~)
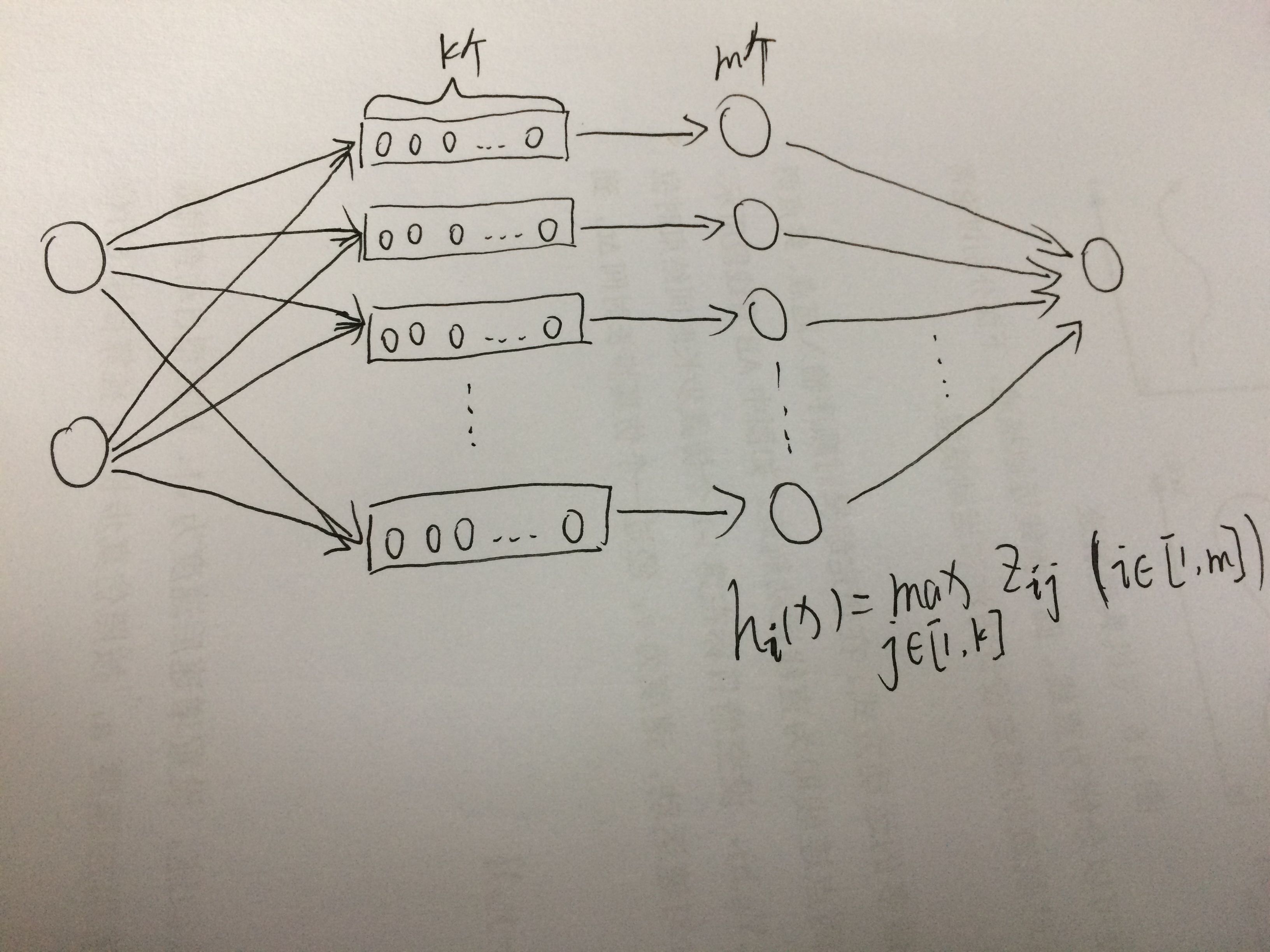
显然,Maxout是一个分段线性函数,而由于任意的凸函数都可由分段线性函数来拟合,所以,Maxout可以拟合任意的凸函数,论文里列出了以下几种图:
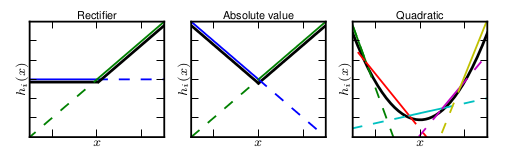
总结:Maxout能拟合任意凸函数,要与Dropout组合使用可以发挥比较好的效果。但是它加入了一个先验:样本集是凸集可分的。